Mathematik an der Universität Göttingen
Suche

Bild Siegel

Carl Ludwig Siegel (1896-1981)





Historisches


Historische Persönlichkeiten Göttingens in der Mathematik

Carl Ludwig Siegel

Carl Ludwig Siegel wurde am 31.12.1896 in Berlin geboren. 1915 erwarb er den Schulabschluß und schrieb sich danach als Student der Mathematik, Astronomie und Physik an der Friedrich-Wilhelm-Universität zu Berlin ein. Bereits in seinem vierten Semester gelang es ihm, den Thue'schen Satz über die Approximation algebraischer Zahlen wesentlich zu verschärfen. Siegel bewies:

"Zu jeder algebraischen Zahl $m \ge n$ vom Grad $m \ge n$ über den rationalen Zahlen gibt es eine positive Zahl $m \ge n$, so daß

$m \ge n$

für alle ganzen, rationalen Zahlen $m \ge n$ und $m \ge n$ gilt".

Kurz darauf wurde sein Studium jedoch durch Einziehung zum Wehrdienst unterbrochen. Erst zum Sommersemester 1919 bezog er die Universität Göttingen und promovierte 1920 bei Landau mit seinem bereits in Berlin gefundenen Ergebnis. Nach kurzer Unterbrechung durch einen Lehrauftrag an der Universität Hamburg war er weitere drei Semester als Assistent von Courant in Göttingen. Aus dieser Zeit stammt eine Reihe bedeutender Arbeiten, aus der algebraischen und analytischen Zahlentheorie, die den jungen Gelehrten rasch bekannt machten und dazu führten, daß er 1921 die venia legendi für Mathematik erhielt und bereits 1922 als ordentlicher Professor für Mathematik an die Universität Frankfurt berufen wurde. 1938 ging Siegel nach Göttingen und 1940 über Norwegen in die USA, wo er am Institute for Advanced Study in Princeton eine Wirkungsstätte fand. 1951 wurde er auf einen freigewordenen Lehrstuhl an die Universität Göttingen zurückberufen und hier 1959 emeritiert. Bis zu seinem Tode am 4. April 1981 lebte er weiterhin in Göttingen und war auch noch am Mathematischen Institut tätig.

Siegels wissenschaftliches Werk umfaßt bahnbrechende Arbeiten aus verschiedenen Teilen der Mathematik, insbesondere aus Analysis und Zahlentheorie. An seine Dissertation knüpft eine große Arbeit über diophantische Approximationen mit Anwendungen auf diophantische Gleichungen an. Den Ergebnissen aus der analytischen Zahlentheorie folgen grundlegende Arbeiten über die analytische Theorie der quadratischen Formen, die wiederum zu Untersuchungen über Modulfunktionen höheren Grades führten. Diese Funktionen tragen heute seinen Namen und sind zum Gegenstand einer eigenen Theorie geworden. Dieses sei an einem Beispiel erläutert.

Zu Siegel's berühmtesten Arbeiten gehören diejenigen über die analytische Theorie der quadratischen Formen. Eines der wichtigsten Resultate ist die "analytische Klassenformel", welche folgendes besagt:
Für $m \ge n$ sei $A (S,T)$ die Anzahl der Darstellungen der positiv semidefiniten, symmetrischen, ganzzahligen $n \times n$ Matrix $T$ durch die positiv definite, symmetrische, ganzzahlige $m \times m$ Matrix $S$. Die positiv definiten, symmetrischen, ganzzahligen $m \times m$ Matrizen $S_1, \ldots, S_h$ mögen die $h$ Klassen innerhalb des Geschlechtes von $S$ repräsentieren. Man setze

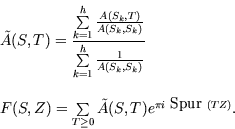
\begin{displaymath}\begin{array}{l} \tilde{A} (S,T) = \displaystyle{\frac{\sum\l... ...0} \tilde{A} (S,T) e^{\pi i ~\mbox{\rm Spur}~ (TZ)}.\end{array}\end{displaymath}

Hierbei ist $Z$ eine komplexe symmetrische $n \times n$ Matrix mit positiv definitem Imaginärteil. Dann lautet die analytische Klassenzahlformel

\begin{displaymath}F(S,Z) = \sum\limits_{(C,D)} \displaystyle{\frac{H (S,C,D)}{\mbox{\rm Det}~ (CZ+D)^{\frac{m}{2}}}}\end{displaymath}

mit einer endlichen Summe $H(S,C,D)$. Summiert wird über ein Repräsentantensystem $(C,D)$ der Klassen symmetrischer teilerfremder Matrizenpaare. Der letzte Ausdruck für $F (S,Z)$ ist eine Eisensteinreihe, die zu den Modulfunktionen höheren Grades gehört. Dieser Zusammenhang mit quadratischen Formen regte Siegel an, die "Siegelschen Modulformen" in die Mathematik einzuführen.

Ein weiteres Arbeitsgebiet war die Himmelsmechanik, der Siegel entscheidende Fortschritte verdankt. In seinem Buch über Himmelsmechanik findet sich sinngemäß der folgende Satz:

"Es lassen sich positive Zahlen $\rho$ und $\epsilon$ finden, so daß bei einem etwaigen Zusammenstoß von Erde und Sonne der Mond mindestens den Abstand $\rho$ von der Erde hat und dann noch mindestens die Zeit $\epsilon$ braucht, bis auch er vielleicht mit ihr zusammenstößt. Dieses Ergebnis wird uns dabei helfen, zuversichtlich in die Zukunft zu schauen".

In seinen Vorlesungen sowie in seinen Veröffentlichungen hat Siegel großen Wert auf die sorgfältige Ausarbeitung bis ins Detail gelegt. Seine Vorlesungen waren wegen ihrer Klarheit berühmt. Er benutzte nie ein Manuskript, sondern trug völlig frei vor, wobei er auch die kompliziertesten Formeln aus dem Gedächtnis beherrschte. Carl Ludwig Siegel war einer der wirklich Großen in der Mathematik dieses Jahrhunderts, und er hat ihre Entwicklung entscheidend beeinflußt. Bei einem solchen Lebenswerk blieben die Ehrungen nicht aus. Carl Ludwig Siegel war Ehrendoktor mehrerer in- und ausländischer Universitäten, Mitglied zahlreicher Akademien und wissenschaftlicher Gesellschaften. 1964 wurde ihm das große Verdienstkreuz mit Stern des Verdienstordens der Bundesrepublik Deutschland verliehen. Eine besondere Ehrung war die 1963 erfolgte Wahl zum Mitglied des Ordens pour le mérite. 1978 wurde ihm der hochdotierte Wolf-Preis verliehen.