Mathematik an der Universität Göttingen

Bild Herglotz

Gustav Herglotz (1881-1953)

Historisches

Historische Persönlichkeiten Göttingens in der Mathematik

Gustav Herglotz

Gustav Herglotz wurde 1881 in Wallern (Böhmen) geboren. 1925 wurde er als Nachfolger von C. Runge nach Göttingen berufen. Er starb 1953 in Göttingen.

Seine Hauptbeiträge liegen auf dem Gebiet der partiellen Differentialgleichungen, der Funktionentheorie und der Differentialgeometrie. Aus dem Kreis seiner funktionentheoretischen Untersuchungen ist die Arbeit: "Über Potenzreihen mit positivem reellen Teil im Einheitskreis" (Leipziger Ber. 63, 1911, 501 - 511) vielleicht die bekannteste. Sie steht in direktem Zusammenhang mit dem trigonometrischen Momentenproblem. Darin wird gezeigt, daß sich jede im Einheitskreis 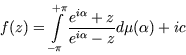$\vert z\vert < 1$ holomorphe Funktion f (z) mit positivem Realteil in der Form

$\begin{displaymath}f(z) = \int\limits^{+ \pi}_{- \pi} \frac{e^{i\alpha } + z}{e^{i\alpha }-z} d \mu(\alpha ) + ic\end{displaymath}$

mit einer monoton-nichtfallenden Funktion µ( $\alpha$ ) und einer reellen Zahl c darstellen läßt. Die am besten bekannte differentialgeometrische Arbeit von Herglotz ist sein Beweis des Cohn-Vossenschen Satzes von der Starrheit der Eiflächen (Abh. Hamburg 15, 127 - 129). Das Problem besteht darin, aus der Gleichheit der ersten Fundamentalformen zweier geschlossener Eiflächen $\varphi_1$ und $\varphi_2$ , d.h. aus

$\begin{displaymath}d \varphi^2_1 = d \varphi^2_2\end{displaymath}$

auf die Gleichheit ihrer zweiten Fundamentalformen zu schließen. Die dem Herglotzschen Beweis zugrundegelegte Integralformel hat sich für die Theorie der Flächenverbiegung als fundamental erwiesen und die weitere Forschung auf diesem Gebiete entscheidend beeinflußt.