Mathematik an der Universität Göttingen
Suche

Bild Gauss

Carl Friedrich Gauß 1777-1855





Historisches


Historische Persönlichkeiten Göttingens in der Mathematik

Carl Friedrich Gauß

Carl Friedrich Gauß wurde am 30. April 1777 in Braunschweig geboren. Er wuchs in bescheidenen Verhältnissen auf, aber seine Lehrer sorgten dafür - gegen den Widerstand des Vaters -, daß er eine höhere Schule besuchen konnte. Als Vierzehnjähriger wurde Gauß dem Herzog von Braunschweig bei Hofe vorgestellt, der beeindruckt von den Rechenkünsten des Knaben, von da an für seinen Unterhalt sorgte. Dadurch wurde Gauß die Ausbildung am herzoglichen Collegium Carolinum und das Studium in Göttingen ermöglicht, anschließend konnte er sich bis zum Alter von 30 Jahren ganz seinen mathematischen und astronomischen Forschungen widmen. Es war die fruchtbarste Periode seines Schaffens mit einer ungeheuren Fülle an Ideen und Resultaten, die man zum großen Teil erst nach seinem Tod bei der Bearbeitung seines Nachlasses entdeckte, Gauß veröffentlichte erst dann etwas, wenn es die von ihm angestrebte vollkommene Form hatte, gemäß seinem Grundsatz "Pauca sed matura" oder zu deutsch "Wenig aber Reifes".

Die erste große Frucht dieser Zeit ab 1796 waren die "Disquisitiones Arithmeticae", mit denen er die moderne Zahlentheorie begründete und mit dessen Erscheinen im Jahre 1801 Gauß sofort in die Reihe der führenden Mathematiker aufrückte. über mathematische Fachkreise hinaus berühmt wurde er, als Anfang 1802 der Planetoid Ceres an dem von ihm vorausberechneten Ort wiedergefunden wurde, die Suche nach diesem von dem italienischen Astromomen Piazzi kurzzeitig beobachteten, dann aber wieder verlorengegangenen Kleinplaneten wurde damals von der wissenschaftlichen Welt mit starkem Interesse verfolgt. Seine Bahnberechnungsmethoden setzte Gauß in der 1809 erschienenen "Theoria Motus Corporum Coelestium" auseinander, sie sind bis heute zwar etwas modifiziert, insbesondere der Benutzung moderner Rechenanlagen angepaßt, aber im Kern nicht mehr verbessert worden. 1807 wurde Gauß Direktor der Sternwarte der Universität Göttingen und in dieser Stellung blieb er bis zu seinem Tod im Jahre 1855 trotz verlockender Angebote von auswärts. In fast 50 Jahren seines Wirkens in Göttingen betrieb er nicht allein seine mathematischen und astronomischen Forschungen.

1820 regte er die hannoversche Landesvermessung an und trug in den ersten Jahren die Hauptlast dieser Aufgabe fast auf sich allein gestellt. Unter großen Strapazen führte er die Messungen im Felde durch und auch die Auswertung lag ganz in seinen Händen. Nebenbei entwickelte er dabei den Heliotropen, noch lange Zeit ein unentbehrliches Arbeitsgerät des Geodäten. Später untersuchte er zusammen mit Wilhelm Weber Elektrizität und Magnetismus, wobei als Nebenprodukt der elektrische Telegraph entstand. Die Mathematik aber, insbesondere die Arithmetik, stand bei ihm an höchster Stelle, in einem Brief an Gerling vom 6. Januar 1819 schreibt er: "Für mich wenigstens sind und bleiben die Untersuchungen der höheren Arithmetik, bei weitem das Allerschönste der Mathematik, und der Genuss, den ich, auch an der schönsten astronomischen Untersuchung finde, ist gar Nichts, verglichen mit dem, welchen die höhere Arithmetik gewährt".

Am 29. März 1796 ("ehe ich aus dem Bett aufgestanden war") entdeckte Gauß, daß die Konstruktion des regelmäßigen 17-Eck mit Zirkel und Lineal möglich ist, und das gab den letzten Anstoß dafür, daß er sich der Mathematik verschrieb, vorher hatte er noch die Möglichkeit erwogen, sich dem Studium der alten Sprachen zu widmen. Gauß' überlegungen gingen aber weit über die Konstruktion des 17-Ecks hinaus, er bewies, daß für eine ungerade Primzahl $p$ sich das regelmäßige $p$-Eck genau dann mit Zirkel und Lineal konstruieren läßt, wenn

\begin{displaymath}p = 2^{2^m} + 1\end{displaymath}

ist mit einer nichtnegativen ganzen Zahl $m$. So ist auch das regelmäßige 257 und das 65537-Eck mit Zirkel und Lineal konstruierbar.

Für das bereits von Euler vermutete Quadratische Reziprozitätsgesetz


\begin{displaymath}\Bigl(\frac{p}{q}\Bigr) \cdot \Bigl(\frac{q}{p}\Bigr) = (-1)^{ \frac{p-1}{2} \frac{q-1}{2}} \end{displaymath}

gab Gauß den ersten stichhaltigen Beweis. Dabei sind $p$ und $q$ zwei ungerade verschiedene Primzahlen und das Legendre-Symbol $(\frac{p}{q})$ ist gleich 1, falls $p$ quadratischer Rest modulo $q$ ist, und es ist $-1$ im anderen Fall. Gauß kam auf dieses Thema immer wieder zurück, acht verschiedene Beweise hat er für diesen Satz gefunden, von denen jeder Keim wichtiger Entwicklungen wurde, die sich bis in die heutige Zeit verfolgen lassen.

In seinen "Notizenjournal", einem mathematischen Tagebuch, notierte Gauß am 10. Juli 1796

"E Y P H K A num. $= \Delta + \Delta + \Delta$".

Heureka (ich hab's gefunden): Jede positive ganze Zahl ist Summe von drei Dreieckszahlen (das sind Zahlen der Form $\frac{m (m+1)}{2}$ mit ganzem $m$). Gauß gelang es, für diese berühmte, von Fermat ausgesprochene Tatsache den ersten strengen Beweis zu liefern.

Die komplexen Zahlen deutete Gauß als Punkte einer Ebene, heute spricht man von der Gaußschen Ebene. Erst diese geometrische Veranschaulichung und die Autorität Gauß' brachten den komplexen Zahlen die volle Anerkennung als mathematische Objekte.

In seiner Dissertation gab Gauß 1799 den ersten vollständigen Beweis für den Fundamentalsatz der Algebra: Jedes Polynom über den komplexen Zahlen vom Grade $n \ge 1$ läßt sich in Linearfaktoren zerlegen.

Seine astronomischen Bahnberechnungen führten Gauß zur Untersuchung der hypergeometrischen oder Gaußschen Reihe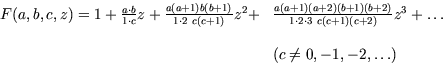

\begin{displaymath}\begin{array}{ll} F(a,b,c,z) = 1+ \frac{a \cdot b}{1 \cdot c}... ...c+2)} z^3 + \ldots\\ \\ & (c \neq 0,-1,-2, \ldots)\end{array}\end{displaymath}

Er berechnete

\begin{displaymath}F(a,b,c,1) = \frac{\Pi (c-1) \Pi (c-a-b-1)}{\Pi (c-a-1) \Pi (c-b-1)}, \quad \mbox{falls Re}~ (c-a-b) > 0,\end{displaymath}

und konnte damit das Umlaufverhalten von $w = F (a,b,c,z)$ als Lösung der hypergeometrischen oder Gaußschen Differentialgleichung

\begin{displaymath}z(1-z) w" + (c- (a+b+1)z)w' - abw=0\end{displaymath}

um die singulären Punkte $0,1$ und $\infty$ beschreiben. Die Fakultät $\Pi (z)$ - eng verwandt mit der Gammafunktion, nämlich $\Pi (z) = \Gamma (z+1)$ - führte er ein durch

\begin{displaymath}\Pi (z) = \lim\limits_{n \to \infty} \frac{1 \cdot 2 \cdot \ldots \cdot n}{(z+1)(z+2) \cdot \ldots \cdot (z+n)} n^z.\end{displaymath}

Er behandelte $F(a,b,c,z)$ und $\Pi (z)$ als analytische Funktionen der komplexen Variablen $z$. Aus einem berühmten Brief an Bessel geht hervor, daß er bereits 1811 im Besitz entscheidender Grundprinzipien der komplexen Analysis war, er erklärt dort mit wenigen Worten Kurvenintegrale und formuliert den Cauchyschen Integralsatz.

Die Beschäftigung mit der Geodäsie führte Gauß zur Untersuchung krummer Flächen im dreidimensionalen euklidischen Raum. Nachdem er ein Krümmungsmaß erklärt hat, heute spricht man von der Gaußschen Krümmung, gipfeln seine überlegungen in dem Theorema egregium: Die Gaußsche Krümmung bleibt erhalten bei einer längentreuen Abbildung der Fläche. Den Beweis führt er, indem er die Krümmung allein durch die Fundamentalgrößen $E,F$ und $G$ der Fläche ausdrückt, nämlich

\begin{displaymath}\begin{array}{c} 4 ( EG - F^2 )^2\cdot k\\ \\ = E \Biggl[ \... ...tial q} + \frac{\partial^2 G}{\partial p^2} \Biggr] \end{array}\end{displaymath}

sie hängt also nur von den "inneren" Eigenschaften der Fläche ab. Dieser Gedanke wurde später von Riemann aufgegriffen und weiterentwickelt; am Ende dieser Entwicklung steht Einsteins Relativitätstheorie.

Gauß hat immense numerische Berechnungen durchgeführt, zeitweise schrieb er monatelang Tag für Tag rund 4000 Ziffern nieder. Dabei diente ihm das Gaußsche Eliminationsverfahren zur Aufläsung linearer Gleichungssysteme und das Gaußsche Quadraturverfahren zur numerischen Integration. Zur Auswertung von Maßreihen erfand er die Methode der kleinsten Quadrate und das Gaußsche Fehlergesetz.

Immer wieder forderte Gauß die Strenge der "alten Geometer", also die Herleitung mathematischer Aussagen aus wenigen Grundtatsachen wie bei Euclid, die von ihm gesetzten Maßstäbe an Strenge und Stil haben die Mathematik bis heute geprägt.