Mathematik an der Universität Göttingen

Bild Riemann

Bernhard Riemann (1826-1866)

Historisches

Historische Persönlichkeiten Göttingens in der Mathematik

Bernhard Riemann

Bernhard Riemann wurde am 17. September 1826 in Breselenz bei Dannenberg nahe der Elbe geboren und stammte aus einem lutherischen Pastorenhaus. Seine mathematischen Neigungen zeigen sich früh, trotzdem ergreift er 1846, dem Wunsch des Vaters folgend, zunächst das Studium der Theologie und Philosophie in Göttingen. Dabei hörte er auch mathematische Vorlesungen, und er durfte sich bald mit dem Einverständnis seines Vaters ganz der "brotlosen Mathematik" zuwenden.

Während des Studiums in Göttingen und Berlin, gefördert von Dirichlet, Wilhelm Weber und Gauß, zeigte sich bereits die Tiefe und Kraft seines Genies. Es war eine Sternstunde der Mathematik als der junge Riemann dem legendären Gauß in seinem Habilitationsvortrag am 10. Juni 1854 seine "Hypothesen, welche der Geometrie zu Grunde liegen" auseinandersetzte, ohne eine einzige Formel zu benutzen. Gauß, der aus den drei vorgeschlagenen Themen zur überraschung Riemanns gerade dies ausgewählt hatte, war damals wohl der einzige, der Riemanns Gedanken voll würdigen konnte. Die Riemannsche Geometrie bildet das Fundament der Differentialgeometrie und der allgemeinen Relativitätstheorie Einsteins.

1859 wurde Riemann Nachfolger des früh verstorbenen Dirichlet auf dem Lehrstuhl, den zuvor Gauß innegehabt hatte. In der kurzen Zeit bis zu seinem Tod schuf Riemann bahnbrechende Arbeiten zur Theorie der analytischen Funktionen, zur analytischen Zahlentheorie und zur mathematischen Physik. Seine umwälzenden Ideen wurden erst allmählich verstanden, aber sie haben die Entwicklung der Mathematik um so nachhaltiger beeinflußt und wirken noch heute richtungsweisend.

Schon im Jahre 1862 verschlechterte sich Riemanns Gesundheitszustand zusehends. Er litt an Tuberkulose, der man damals noch hilflos gegenüberstand. Mehrere Aufenthalte im milden Klima Italiens konnten die Auswirkungen der Krankheit vielleicht etwas mildern, aber nur 39 Jahre alt starb Riemann am 20. Juli in Selasca am Lago Maggiore.

In seiner einzigen, nur acht Seiten langen zahlentheoretischen Arbeit liefert Riemann den Schlüssel zu Fragen über die Verteilung der Primzahlen, indem er diese mit der analytischen Funktion

$\begin{displaymath}\zeta (s) = 1+ \frac{1}{2^s} + \frac{1}{3^s} + \ldots , ~\mbox{Re}~ (s) >1,\end{displaymath}$

verknüpft, welche heute Riemannsche Zetafunktion genannt wird. Er zeigte, daß die Funktion sich in die ganze Ebene holomorph fortsetzen läßt mit Ausnahme eines Pol 1. Ordnung bei

und daß sie der Funktionalgleichung

$\begin{displaymath}\pi^{-\frac{s}{2}} \Gamma \Bigl(\frac{s}{2}\Bigr) \zeta (s) = \pi^{-\frac{1-s}{2}}\Gamma \Bigl(\frac{1-s}{2}\Bigr) \zeta (1-s)\end{displaymath}$

genügt.

Riemann hatte vor allem eine Beziehung zwischen der Zetafunktion und der Primzahlfunktion

$\pi (x)$ im Auge, $\pi (x)$ ist die Anzahl der Primzahlen unterhalb der positiven Zahl

. Er bildete die Funktion

$\begin{displaymath}f(x) = \pi (x) +\frac12\pi\Bigl(x^{\frac12}\Bigr)+\frac13 \pi... ...= \sum\limits^{\infty}_{n=1} \frac{1}{n} \pi (x^{\frac{1}{n}}),\end{displaymath}$

aus der sich mit Hilfe der Möbiusschen $\mu$ -Funktion umgekehrt $\pi (x)$ wieder berechnen läßt, nämlich

$\begin{displaymath}\pi (x) = f(x) - \frac12 f (x^{\frac12}) - \frac13 f (x^{\fra... ...um\limits^{\infty}_{n=1} \frac{\mu (n)}{n} f (x^{\frac{1}{n}}).\end{displaymath}$

Dann stellte er seine Hauptformel auf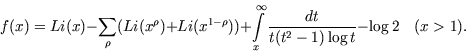

$\begin{displaymath}f(x) = Li (x) - \sum\limits_{\rho} (Li (x^{\rho}) + Li (x^{1-... ...ts^\infty_x \frac{dt}{t (t^2-1) \log t} - \log 2 \quad (x > 1).\end{displaymath}$

Dabei ist $Li(x) = \int^x_0 \frac{dt}{\log t}$ der Integrallogarithmus, und die Summe wird erstreckt über alle Nullstellen $\rho$ der Zetafunktion in dem "kritischen Streifen" Re mit positivem Imaginärteil. Den Beweis für diese Formel führte von Mangoldt im Jahre 1895.

Die Hauptformel liefert eine Möglichkeit $\pi (x)$ zu berechnen, vorausgesetzt man "kennt" die Nullstellen der Zetafunktion im kritischen Streifen. Riemann vermutete, daß diese Nullstellen sämtlich auf der kritischen Geraden Re $(s)= \frac12$ liegen und fügte lapidar hinzu: "Hiervon wäre allerdings ein strenger Beweis zu wünschen; ich habe indes die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da es für den nächsten Zweck meiner Untersuchung entbehrlich schien". Heute spricht man von der Riemannschen Vermutung. Sie hat bis jetzt allen Beweis- und Widerlegungsversuchen getrotzt. Eine Antwort würde unser Wissen über die Verteilung der Primzahlen erheblich erweitern.

Den Begriff der analytischen Funktion stellte Riemann auf eine sichere Grundlage, indem er ihn durch lokale Eigenschaften erklärte, nämlich dadurch, daß die vermittelte Abbildung (außer in einigen Ausnahmepunkten) konform ist oder daß Real- und Imaginärteil der Funktion die Cauchy-Riemannschen Differentialgleichungen erfüllen

$\begin{displaymath}\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x}.\end{displaymath}$

Mit Hilfe des "Dirichletschen Prinzips", das später von Weierstraß kritisiert wurde, dessen Benutzung in diesem Fall dann aber von Hilbert gerechtfertigt wurde, bewies Riemann in seiner Dissertation 1851, daß sich jedes einfach zusammenhängende Gebiet der komplexen Ebene mit Ausnahme der vollen Ebene durch eine holomorphe Funktion bijektiv auf das Innere des Einheitskreises abbilden läßt. Das ist der Riemannsche Abbildungssatz.

Aus dem Dschungel von Schwierigkeiten, die bei der Behandlung mehrdeutiger analytischer Funktionen auftreten, wies Riemann den Ausweg, indem er für solche Funktionen Riemannsche Flächen als Definitionsbereich benutzte. Dieser Begriff erhellte die Untersuchungen des vorhergehenden halben Jahrhunderts über algebraische Kurven, vereinheitlichte sie und öffnete den Weg für künftige große Entwicklungen.

Riemann untersuchte die meromorphen Funktionen auf einer kompakten Riemannschen Fläche vom Geschlecht , die höchstens an vorgegebenen Stellen einfache Pole besitzen, und zeigte, daß diese Funktionen einen Vektorraum über den komplexen Zahlen bilden, dessen Dimension endlich, aber mindestens ist. Das ist der Kern des Satzes von Riemann und Roch, der zusammen mit seinen Varianten eine zentrale Rolle spielt in der komplexen Analysis und algebraischen Geometrie.